1619. Prize collection
In a video
game, n prize boxes are
arranged in a row. Each box contains a certain number of points. According to
the game rules, you cannot choose adjacent boxes – if two neighboring boxes are
opened, the alarm system will trigger, and you will lose all the prizes.
Given the
number of points in each box, determine the maximum number of points you can
collect without triggering the alarm.
Input. The first line contains the number of boxes n (1 ≤ n ≤ 106). The second line contains n non-negative integers a1, a2, ..., an,
where ai is the number of
points that can be obtained from the i-th
box.
Output. Print the maximum number
of points that can be collected without triggering the alarm.
![]()
|
Sample
input |
Sample
output |
|
5 6 1 2 10 4 |
16 |
SOLUTION
dynamic programming
Algorithm analysis
Let’s number the boxes
starting from the first one (the i-th box contains ai points). Let f(i) denote the maximum sum of points that can be obtained by considering the
boxes from the first to the i-th, inclusive.
Then:
·
f(1) = a1,
·
f(2) = max(a1,
a2)
When computing f(i), consider two cases:
·
If the i-th box is chosen, the neighboring (i – 1)-th box cannot be selected. In
this case, the maximum sum of points will be f(i – 2) + ai.
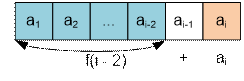
·
if the i-th box is
not chosen, the maximum sum of points equals f(i – 1).

Thus,
f(i) = max(f(i – 2) + ai, f(i – 1))
Let’s store the values of
f(i) in the array res. The
answer to the problem will be the value f(n)
= res[n].
Example
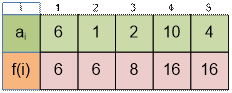

Let us compute f(3)
If we do not open the
third box, then we simply take the best result for the first two boxes: f(2) = 6.
If we open the third box,
then we cannot open the second one (they are adjacent). Therefore, we take the
optimal result for the first box and add the points from the third box:
f(1) + a3
= 6
+ 2 = 8
Ñhoose the maximum of the
two options:
f(3) = max(f(2), f(1) + a3)
= max(6, 8) = 8
Let us compute f(4)
If we do not open the
fourth box, then the result equals f(3) = 8.
If we open the fourth box,
then we cannot open the third one. So we take the best result for the first two
boxes and add the points from the fourth box:
f(2) + a4
= 6
+ 10 = 16
Ñhoose the maximum of the
two options:
f(4) = max(f(3), f(2) + a4)
= max(8, 16) = 16
Exercise
Compute the values of f(i) for the following input data:
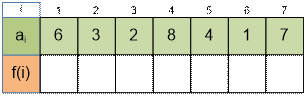
Algorithm implementation
Declare the input array à and the resulting array res.
#define MAX 1000001
long long
a[MAX], res[MAX];
Read the input data.
scanf("%d",&n);
for (i = 1; i <= n; i++)
scanf("%lld",&a[i]);
Compute the answer res1
for one box, and res2 for
two boxes.
res[1] = a[1];
if (n > 1) res[2] = max(a[1],a[2]);
Compute the answers for the remaining boxes.
for (i = 3; i <= n; i++)
res[i] = max(res[i - 2] + a[i], res[i - 1]);
Print the answer.
printf("%lld\n",res[n]);
Java implementation
import java.util.*;
class Main
{
static long a[] = new long[1000001];
static long res[] = new long[1000001];
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
for (int i = 1; i <= n; i++)
a[i] = con.nextInt();
res[1] = a[1];
if (n > 1) res[2] = Math.max(a[1],a[2]);
for (int i = 3; i <= n; i++)
res[i] = Math.max(res[i - 2] + a[i], res[i - 1]);
System.out.println(res[n]);
con.close();
}
}
Python implementation
Read the input data.
n = int(input())
lst = list(map(int,input().split()))
Initialize the list dp.
dp = [0] * len(lst)
Compute the answer dp0 for one box, and dp1 for two boxes.
dp[0] = lst[0]
if (n > 1): dp[1] = max(lst[0], lst[1])
Compute the answers for the remaining boxes.
for i in range(2, len(lst)):
dp[i] = max(dp[i-1], dp[i-2] + lst[i])
Print the answer.
print(dp[-1])